Barlow Twins

Barlow Twins: Self-Supervised Learning via Redundancy Reduction

• Arxiv link
• PDF Link

This paper offers a new way to do self supervised learning. Previously this is usually done with Contrastive learning, like SIMCLR or CLIP. Or using asymmetric network structure with stop-gradient, like BYOL. The new method is sound on math (unlike BYOL), easy to implement, does not require large batches, and has relatively good result.

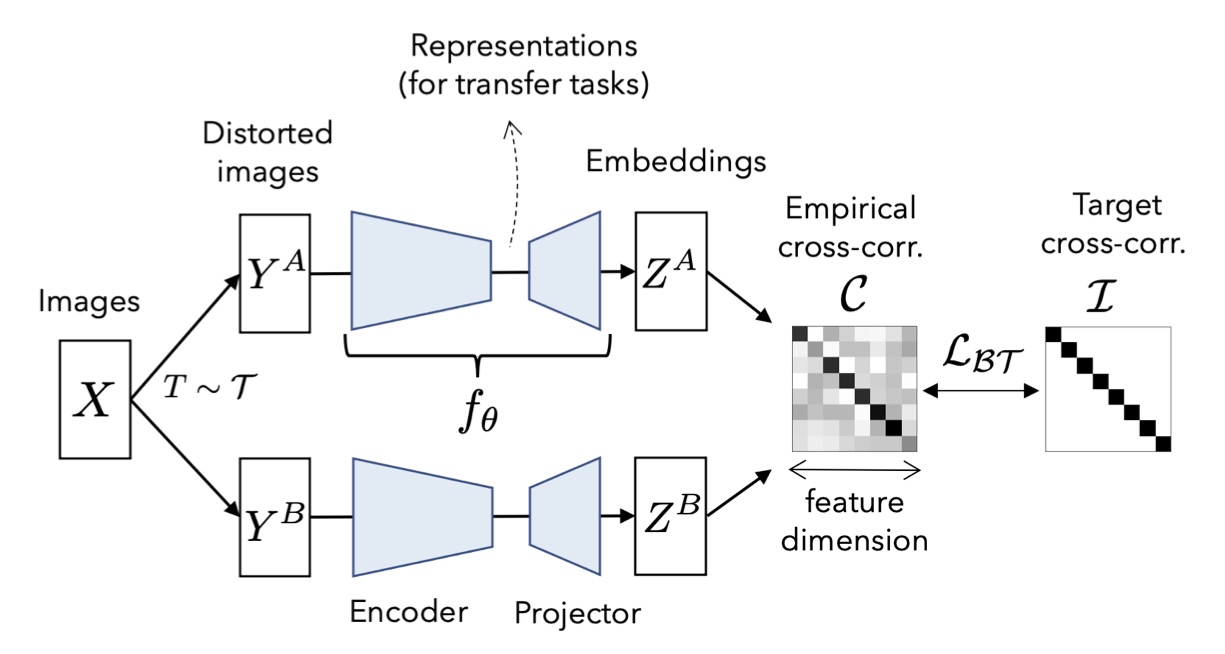
BARLOW TWINS operates on a joint embedding of distorted images. More specifically, it produces two distorted views for all images of a batch $X$ sampled from a dataset. The distorted views are obtained via a distribution of data augmentations $T$ . The two batches of distorted views $Y^A$ and $Y^B$ are then fed to a function $f_{\theta }$ , typically a deep network with trainable parameters $\theta$, producing batches of embeddings $Z^A$ and $Z^B$ respectively. To simplify notations, $Z^A$ and $Z^B$ are assumed to be meancentered along the batch dimension, such that each unit has mean output 0 over the batch.

The most important bit is this loss function:

$$L_{BT}=\sum _i(1-C_{ii}{)}^2+\lambda \sum _i\sum _{j\ne i}{C}_{ij}^2$$

The first part is invariance term, and the second part is the redundancy reduction term. $C$ is the cross-correlation matrix computed between the outputs of the two identical networks along the batch dimension.

So intuitively we want embedding from the same pair has a high correlation, and the ones from different pair does not have much correlation. Note that’s not the same as the INFONCE loss commonly used in contrastive learning method. That one focus on the pair wise distance, or, cosine similarity between the embeddings, but not the overall correlation. In that sense, Barlow twins is more flexible since the distance can be large, as long as the produced embedidings are highly corrlelated. For a more detailed explanation, see The discussion in the paper.

Now let’s come back and write out what’s in $C$.

$$C=\frac{{\sum }_b{z}_{b,i}^A{z}_{b,j}^B}{\sqrt{{\sum }_b(z_{b,i}^A{)}^2}\sqrt{{\sum }_b(z_{b,j}^B{)}^2}}$$

where $b$ indexes batch samples and $i,j$ index the vector dimension of the networks’ outputs. $C$ is a square matrix with size the dimensionality of the network’s output, and with values comprised between $-1$ (i.e. perfect anti-correlation) and $1$ (i.e. perfect correlation).

Pseudo code §

# f: encoder network 
# lambda: weight on the off-diagonal terms 
# N: batch size 
# D: dimensionality of the embeddings 
# 
# mm: matrix-matrix multiplication 
# off_diagonal: off-diagonal elements of a matrix 
# eye: identity matrix
 
for x in loader: # load a batch with N samples 
	# two randomly augmented versions of x 
	y_a, y_b = augment(x)
 
	# compute embeddings 
	z_a = f(y_a) # NxD 
	z_b = f(y_b) # NxD
 
	# normalize repr. along the batch dimension 
	z_a_norm = (z_a - z_a.mean(0)) / z_a.std(0) # NxD 
	z_b_norm = (z_b - z_b.mean(0)) / z_b.std(0) # NxD
 
	# cross-correlation matrix 
	c = mm(z_a_norm.T, z_b_norm) / N # DxD
 
	# loss 
	c_diff = (c - eye(D)).pow(2) # DxD 
	# multiply off-diagonal elems of c_diff by lambda 
	off_diagonal(c_diff).mul_(lambda) loss = c_diff.sum()
 
	# optimization step 
	loss.backward() 
	optimizer.step()

Implementation details §

• It uses 5 augmentation on image, and it’s important that we use them all
• Optimization is complicated. It follows BYOL, uses LARS optimizer with learning rate warmup and cosine decay schedule.