Two Step CCA

Arxiv Link PDF Link

The goal: learn a low level embedding in an unsupervised learning way. E.g. get word embedding.

CCA §

CCA is the analog to Principal Component Analysis (PCA) for pairs of matrices. PCA computes the directions of maximum covariance between elements in a single matrix, whereas CCA computes the directions of maximal correlation between a pair of matrices.

So if we got two metrics $L$ and $R$, we would like to simultaneously find the directions ${\Phi }_l$ and ${\Phi }_r$ that maximize the correlation of the projections of $L$ onto ${\Phi }_l$ with the projections of $R$ onto ${\Phi }_r$. Writing it in formula:

$$\underset{{\Phi }_l,{\Phi }_r}{\max }\frac{\mathbb{E}[⟨L,{\Phi }_l⟩⟨R,{\Phi }_r⟩]}{\sqrt{\mathbb{E}[⟨L,{\Phi }_l{⟩}^2]\mathbb{E}[⟨R,{\Phi }_r{⟩}^2]}}$$

Here the expectation is assuming $L$ and $R$ are datasets.

OSCCA (One Step CCA) §

TL; DR: $\text{CCA}(C,W)\to ({\Phi }_C,{\Phi }_W)$

• $v$: vocabulary size
• $n$: the number of tokens in the document. We can represent the document by $\{w_1,w_2,...,w_n\}$
• $h$: Left and right context size.

Recall the goal is to find a mapping from $v$ dimension to $k$ dimension. This is what we call eigenword dictionary. We then have context matrices $L_{n\times vh}$ and $R_{n\times vh}$, and the tokens themselves, $W_{n\times v}$. What’s stored in each row is a one-hot encoding. In $W$, we represent the presence of the $j^{th}$ word type in the $i^{th}$ position in a document by setting matrix element $w_{ij}=1$.

Create the context $C$ as the concatenation $[LR]$. So on each row you got flattened context.

We then can tell the following (not used in the method though):

• $A_{CW}=C^{T}W$ contains the counts of how often each word $w$ occurs in each context $c$.
• $A_{CC}=C^{T}C$ gives the covariance of contexts.
• $A_{WW}=W^{B}W$ is the word covariance matrix, a diagonal matrix with the counts of each word on the diagonal. Why? It’s like summation across document.

Then we try to find the projections operated on both context and tokens, such that they have maximal correlation. The projection space we choose has dimension $k$. The intuition is that the context and the token themselves should represent the same thing. $\text{CCA}(C,W)\to ({\Phi }_C,{\Phi }_W)$ There’s a way to compute $\Phi$, see the paper for detalis.

TSCCA §

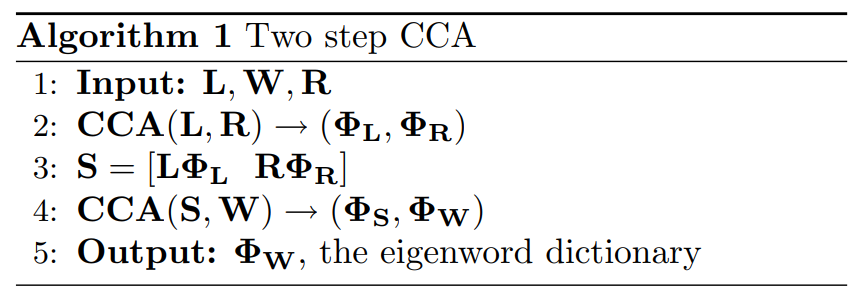
So we first use left and right context to get a state $S$, then do another CCA on $W$.

The two step method requires fewer tokens of data to get the same accuracy in estimating the eigenword dictionary because its final step estimates fewer parameters $O(vk)$ than the OSCCA does $O(v^2)$.

Before stating the theorem, we first explain this intuitively. Predicting each word as a function of all other word combinations that can occur in the context is far sparser than predicting low dimensional state from context, and then predicting word from state. Thus, for relatively infrequent words, OSCCA should have significantly lower accuracy than the two step version. Phrased differently, mapping from context to state and then from state to word (TSCCA) gives a more parsimonious model than mapping directly from context to word (OSCCA).