Class-Balanced Loss

Summary §

A new way to apply weighting to loss for class imbalanced dataset. It’s a middle ground between no-weighting and by inverse class frequency. When used with Focal loss, it can be viewed as an explicit way to set ${\alpha }_t$ .

How to use §

Pick a $\beta$, let’s say 0.999, and weight category loss by $\frac{1-{\beta }^n}{1-\beta }$, where $n$ is the number of samples.

Where does this come from? §

The paper uses set overlapping yada yada. But really it tries to estimate “given this new data, what’s the probability it’s a duplicate and doesn’t matter? Exclude that part and do upsampling for the rest”.

So assume the whole set (for this category) should have $N$ data. Note that noone really know what this $N$ is. The author basically use cross validation to get a “good enough” one. We name “Effective Number” to be “expected volume of samples”. That means “if we have $n$ samples”, theres’ duplicate there, so it would not really cover $n$ volume, the volume would be $E_n$.

And we can prove that

$$E_n=\frac{1-{\beta }^n}{1-\beta }\text{where}\beta =\frac{N-1}{N}$$

the assumption here is if all these samplings are just covering a big set of $N$ (this assumption was not made in other literature), then every time you add a sample, the probability of it overlaps with any existing sample is $p=\frac{E_{n-1}}{N}$.

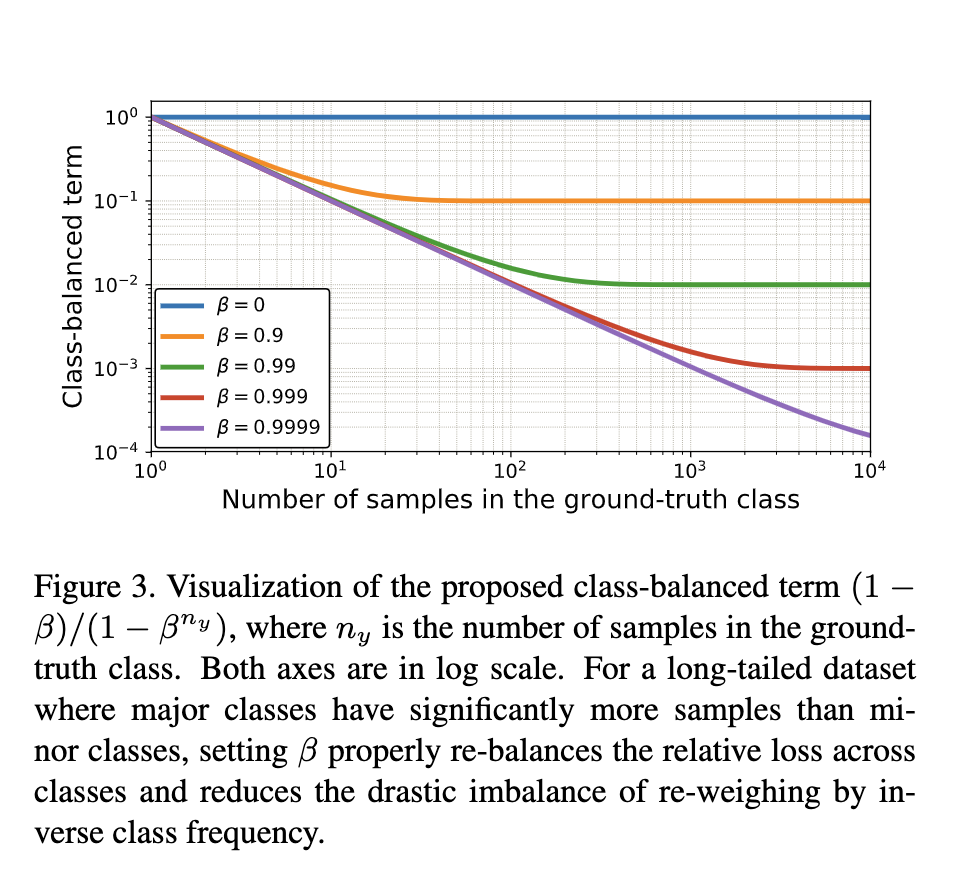
How to pick $\beta$ §

This is reasonable because β = (N − 1)/N , so larger β means larger N . As discussed in Section 3, N can be inter- preted as the number of unique prototypes. A fine-grained dataset should have a smaller N compared with a coarse- grained one. For example, the number of unique prototypes of a specific bird species should be smaller than the number of unique prototypes of a generic bird class. Since classes in CIFAR-100 are more fine-grained than CIFAR-10, CIFAR- 100 should have smaller N compared with CIFAR-10.

class_balanced_loss, page 7